nomadventures.blogg.se - Finding cdf from pdf

#Finding cdf from pdf pdf#

#Finding cdf from pdf pdf#

Problem 6.2.1 Solution We are given that W X +Y and that the joint PDF of X and Y is fX,Y (x,y) 2 0 x y 1 0 otherwise (1) We are asked to nd the PDF of W. The following graphs illustrate these distributions.The rst step is to nd the CDF of W, FW(w). In this chapter and the next, we will study the uniform distribution, the exponential distribution, and the normal distribution. When using a continuous probability distribution to model probability, the distribution used is selected to model and fit the particular situation in the best way. There are many continuous probability distributions. When we use formulas to find the area in this textbook, the formulas were found by using the techniques of integral calculus. In general, integral calculus is needed to find the area under the curve for many probability density functions. We will find the area that represents probability by using geometry, formulas, technology, or probability tables.

P(c < x < d) is the same as P(c ≤ x ≤ d) because probability is equal to area.

Since the probability is equal to the area, the probability is also zero. The area below the curve, above the x-axis, and between x = c and x = c has no width, and therefore no area (area = 0).

P(x = c) = 0 The probability that x takes on any single individual value is zero.

P(c < x < d) is the area under the curve, above the x-axis, to the right of c and the left of d.

P(c Probability is found for intervals of x values rather than for individual x values.

The entire area under the curve and above the x-axis is equal to one.

The outcomes are measured, not counted.

Probability thus can be seen as the relative percent of certainty between the two values of interest. Remember that the area under the pdf for all possible values of the random variable is one, certainty. Mathematically, the cumulative probability density function is the integral of the pdf, and the probability between two values of a continuous random variable will be the integral of the pdf between these two values: the area under the curve between these values. The cumulative distribution function is used to evaluate probability as area. f( x) is the function that corresponds to the graph we use the density function f( x) to draw the graph of the probability distribution.Īrea under the curve is given by a different function called the cumulative distribution function (abbreviated as cdf). We use the symbol f( x) to represent the curve.

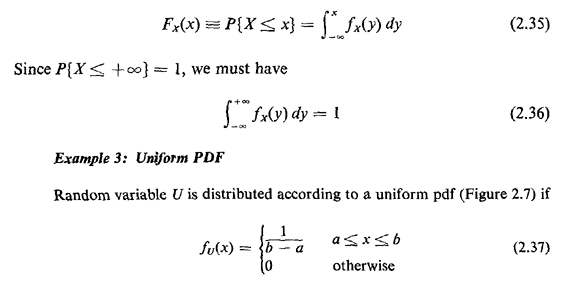
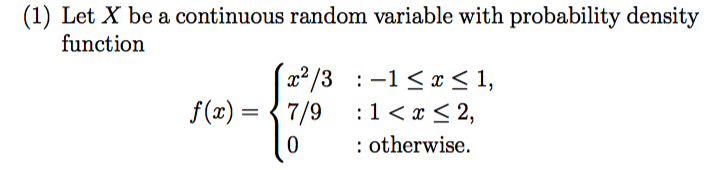
The curve is called the probability density function (abbreviated as pdf). The probability of a specific value of a continuous random variable will be zero because the area under a point is zero. Notice that the horizontal axis, the random variable x, purposefully did not mark the points along the axis. In this case, we were being a bit casual because the random variables of a Poisson distribution are discrete, whole numbers, and a box has width. Again with the Poisson distribution in Chapter 4, the graph in Example 4.14 used boxes to represent the probability of specific values of the random variable. The relative area for a range of values was the probability of drawing at random an observation in that group.

We have already met this concept when we developed relative frequencies with histograms in Chapter 2. Probability is represented by area under the curve. The graph of a continuous probability distribution is a curve. Continuous Random Variables 26 Properties of Continuous Probability Density Functions